本场比赛出题周期里,由于在备赛冲击奖牌,就把这场第二届迎新杯的出题工作基本全交给校队未来的栋梁们了。整个出题过程中,几位学弟们认真负责的态度让我非常放心,事实证明也确实带来了一套不错的题👍从去年叱咤赛场的选手身份转变为尽职尽责的出题人,他们做得很棒!
题号
预估难度
知识点
FirstBlood
A
1 ★
简单数学、容斥原理
ェメ
B
2 ★
二分、数学
clhdlg
C
2 ★
DP动态规划
Ovine
D
3 ★
贪心、优先队列
/
E
2 ★
贪心
ェメ
F
1 ★
思维题
翊,
G
1 ★
贪心、简单模拟
翊,
H
1 ★(签到题)
简单数学
learner_164
I
3 ★
组合数学、推式子
翊,
赛后看了一下,虽然简单了,但也是有区分度的,各个水平的选手也都有题可做,为出题人们点赞!👍
说明:以下所有题解代码,大家关注main函数就行了,代码头部纯属个人习惯,不用深究。
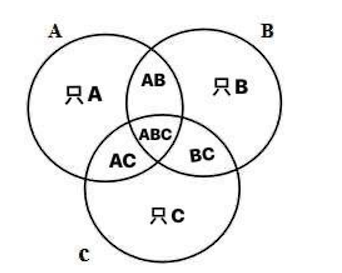
【容斥原理】
首先,我想对于刚高考完的同学来说,整除 这个概念可能有点陌生了。因为大家第一次接触这个词应该是小学初中,高考数学应该是不涉及。
a 被 b 整除 <=> a 除 b 余数为0 <=> a 是 b 的倍数
这道题就是相当于求 1 − n 1-n 1 − n a , b , c a, b, c a , b , c 1 − n 1-n 1 − n x x x n / x n / x n / x n / a + n / b + n / c n / a + n / b + n / c n / a + n / b + n / c
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 #include <bits/stdc++.h> using namespace std;#define pii pair<int, int> #define pdd pair<double, double> #define pll pair<ll, ll> #define debug(x) cerr << #x << ": " << x << '\n' ; #define endl '\n' typedef long long ll;typedef unsigned long long ull;inline void solve () int n, a, b, c; cin >> n >> a >> b >> c; ll res = 0 ; res += n/a + n/b + n/c; res -= n/(a*b) + n/(a*c) + n/(b*c); res += n / (a*b*c); cout << res << endl; } int main () cout << fixed << setprecision (10 ); ios::sync_with_stdio (false ); cin.tie (0 );cout.tie (0 ); int t; cin >> t; while (t --) solve (); return 0 ; }
【二分】k k k 1 e 18 1e18 1 e 1 8 i i i i i i i i i i i i [ 1 , n ] [1, n] [ 1 , n ] k k k n n n k k k 1 e 18 1e18 1 e 1 8 O ( l o g 2 k ) O(log_2{k}) O ( l o g 2 k )
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 #include <bits/stdc++.h> using namespace std;#define pii pair<int, int> #define pdd pair<double, double> #define pll pair<ll, ll> #define debug(x) cerr << #x << ": " << x << '\n' ; #define endl '\n' typedef long long ll;typedef unsigned long long ull;inline void solve () ll k; cin >> k; auto check = [&](ll x) { ll t = sqrt (x); return x - t >= k; }; ll l = 1 , r = 4e18 ; while (l < r) { ll mid = l+r >> 1 ; if (check (mid)) r = mid; else l = mid + 1 ; } cout << l << endl; } int main () cout << fixed << setprecision (10 ); ios::sync_with_stdio (false ); cin.tie (0 );cout.tie (0 ); int t; cin >> t; while (t --) solve (); return 0 ; }
【DP】
前言:去年校赛的云山探险记1也是一个比较典的DP,不过思维难度比本题高一些,欢迎有兴趣的同学去钻研一下(PS:去年那题的定位是防AK,所以一时半会儿没想通也别着急)。
题意就是有一个 n n n
这道题之所以不能直接贪心,是因为我中途可以放弃选一个数,从而使得后续有个原本是第奇数个选中的数,变为第偶数个数,这个数很大的话收获翻倍就能弥补放弃的损失。
还有个值得注意的点是,不会有连续的两个数都不被选中。(从贪心的角度上,这个行为是自损而无利的)
解析直接看代码里的注释
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 #include <bits/stdc++.h> using namespace std;#define pii pair<int, int> #define pdd pair<double, double> #define pll pair<ll, ll> #define debug(x) cerr << #x << ": " << x << '\n' ; #define endl '\n' typedef long long ll;typedef unsigned long long ull;int main () int n; cin >> n; vector<vector<ll>> dp (n+5 , vector <ll>(2 )); vector<int > a (n+1 ) ; for (int i=1 ; i<=n; i++) cin >> a[i]; dp[1 ][1 ] = a[1 ]; dp[1 ][0 ] = -2e18 ; for (int i=2 ; i<=n; i++) { dp[i][0 ] = max (dp[i-1 ][1 ] + a[i]*2 , dp[i-2 ][1 ] + a[i]*2 ); dp[i][1 ] = max (dp[i-1 ][0 ] + a[i], dp[i-2 ][0 ] + a[i]); } cout << max (dp[n][0 ], dp[n][1 ]) << endl; return 0 ; }
解析直接看代码里的注释
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 int main () int n; cin >> n; vector<vector<ll>> dp (n+5 , vector <ll>(2 )); vector<int > a (n+1 ) ; for (int i=1 ; i<=n; i++) cin >> a[i]; dp[1 ][1 ] = a[1 ]; dp[1 ][0 ] = -2e18 ; for (int i=2 ; i<=n; i++) { dp[i][0 ] = max (dp[i-1 ][0 ], dp[i-1 ][1 ] + a[i]*2 ); dp[i][1 ] = max (dp[i-1 ][1 ], dp[i-1 ][0 ] + a[i]); } cout << max (dp[n][0 ], dp[n][1 ]) << endl; return 0 ; }
【贪心】【优先队列】n n n a i a_i a i d i d_i d i
不知道有没有同学看到这道题的时候,想到了最小生成树🤔
这道题怎么贪呢?i i i i i i j j j j j j a j × d j 2 a_j × d_j^2 a j × d j 2 a j × ( d j + 1 ) 2 a_j × (d_j+1)^2 a j × ( d j + 1 ) 2 a j × ( d j + 1 ) 2 − a j × d j 2 a_j × (d_j+1)^2 - a_j × d_j^2 a j × ( d j + 1 ) 2 − a j × d j 2 j j j 优先队列的重载运算符 - octal_zhihao - 博客园
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 #include <bits/stdc++.h> using namespace std;#define pii pair<int, int> #define pdd pair<double, double> #define pll pair<ll, ll> #define endl '\n' typedef long long ll;typedef unsigned long long ull;struct node { ll x; ll y; friend bool operator <(node a,node b) { ll ta = a.x * ((a.y+1 )*(a.y+1 ) - a.y*a.y); ll tb = b.x * ((b.y+1 )*(b.y+1 ) - b.y*b.y); return ta > tb; } }; priority_queue<node> q; inline void solve () int n; cin >> n; vector<ll> a (n+1 ) ; for (int i=1 ; i<=n; i++) cin >> a[i]; sort (a.begin ()+1 , a.end ()); q.push ({a[1 ], 1 }); q.push ({a[2 ], 1 }); ll res = 0 ; res += a[1 ] + a[2 ]; for (int i=3 ; i<=n; i++) { auto [w, d] = q.top (); q.pop (); res += w * ((d+1 )*(d+1 ) - d*d); res += a[i]; q.push ({a[i], 1 }); q.push ({w, d+1 }); } cout << res << endl; } int main () cout << fixed << setprecision (10 ); ios::sync_with_stdio (false ); cin.tie (0 );cout.tie (0 ); solve (); return 0 ; }
【贪心】R i R_i R i ( L , R ) (L, R) ( L , R ) R R R R R R
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 #include <bits/stdc++.h> using namespace std;#define pii pair<int, int> #define pdd pair<double, double> #define pll pair<ll, ll> #define debug(x) cerr << #x << ": " << x << '\n' ; #define endl '\n' typedef long long ll;typedef unsigned long long ull;inline void solve () int n, d; cin >> n >> d; vector<pii> a; for (int i=1 ; i<=n; i++) { int l, r; cin >> l >> r; a.push_back ({l, r}); } sort (a.begin (), a.end (), [&](pii x, pii y) { return x.second < y.second; }); int R = 0 , res = 0 ; for (auto [l, r]: a) { if (l <= R) continue ; res ++; R = r + d - 1 ; } cout << res << endl; } int main () cout << fixed << setprecision (10 ); ios::sync_with_stdio (false ); cin.tie (0 );cout.tie (0 ); solve (); return 0 ; }
【思维】【数学】
过程搞这么复杂,其实*3是不会增加因数分解后2的个数的。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 #include <bits/stdc++.h> using namespace std;#define pii pair<int, int> #define pdd pair<double, double> #define pll pair<ll, ll> #define debug(x) cerr << #x << ": " << x << '\n' ; #define endl '\n' typedef long long ll;typedef unsigned long long ull;int main () int res = 0 ; int n; cin >> n; for (int i=1 ; i<=n; i++) { int a; cin >> a; while (a % 2 == 0 ) { a /= 2 ; res ++; } } cout << res << endl; return 0 ; }
【贪心】【模拟】尽可能地省时 ,那就要尽可能最大化每次右移所打印的数 。
然后规则上,打印机打印了 a a a a + 1 a + 1 a + 1 每次遇到上一个数 + 1 +1 + 1 ,直到无数可印而返回。
这里有个误区就是考虑到DP,但其实每次转移只能到 a + 1 a+1 a + 1
那么回过来,这个逻辑用代码要怎么实现呢?a a a a − 1 a - 1 a − 1 a − 1 a - 1 a − 1 a a a a a a
怎么记录 a − 1 a-1 a − 1 STL 库的 set 容器(不用万能头的话,需要引入set头文件)。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 #include <bits/stdc++.h> using namespace std;#define pii pair<int, int> #define pdd pair<double, double> #define pll pair<ll, ll> #define debug(x) cerr << #x << ": " << x << '\n' ; #define endl '\n' typedef long long ll;typedef unsigned long long ull;int main () int n; cin >> n; set<int > st; int res = 0 ; for (int i=1 ; i<=n; i++) { int ai; cin >> ai; if (!st.count (ai-1 )) res ++; st.insert (ai); } cout << res-1 << endl; return 0 ; }
不用set其实也很简单,用一个bool类型的数组代替就行。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 int main () int n; cin >> n; vector<bool > p (n+1 , false ) ; int res = 0 ; for (int i=1 ; i<=n; i++) { int ai; cin >> ai; if (!p[ai-1 ]) res ++; p[ai] = true ; } cout << res-1 << endl; return 0 ; }
【签到】【模拟】or【数学】b b b a a a [ b , c ] [b, c] [ b , c ]
1 2 3 4 5 6 7 8 9 10 11 12 13 #include <bits/stdc++.h> using namespace std;int main () int a, b, c; cin >> a >> b >> c; if (c < b) c += 24 ; if (a < b) a += 24 ; if (a >= b && a <= c) cout << "No" << endl; else cout << "I love YNU-ICPC team" << endl; return 0 ; }
【组合数学】【推式子】
考了考高中数学的知识,数竞生应该是能拿捏的
性质2: C n 1 + C n 2 + C n 3 + . . . + C n n = 2 n C_{n}^{1}+C_{n}^{2}+ C_{n}^{3}+ ... +C_{n}^{n}= 2^{n} C n 1 + C n 2 + C n 3 + . . . + C n n = 2 n ①
由性质1 可以推出:$m × C_{n}^{m} = n × C_{n-1}^{m-1} $ (展开了约分一下就行)
那么结合性质2可得:1 C n 1 + 2 C n 2 + 3 C n 3 + ⋯ + n C n n = n 2 n − 1 1 C_{n}^{1}+2 C_{n}^{2}+3 C_{n}^{3}+\cdots+n C_{n}^{n}=n 2^{n-1} 1 C n 1 + 2 C n 2 + 3 C n 3 + ⋯ + n C n n = n 2 n − 1
又因为 m 2 × C n m = m × n × C n − 1 m − 1 = n × C n − 1 m − 1 + n × ( m − 1 ) × C n − 1 m − 1 m^2 × C_{n}^{m} = m × n × C_{n-1}^{m-1} = n × C_{n-1}^{m-1} + n × (m-1) × C_{n-1}^{m-1} m 2 × C n m = m × n × C n − 1 m − 1 = n × C n − 1 m − 1 + n × ( m − 1 ) × C n − 1 m − 1
1 2 C n 1 + 2 2 C n 2 + 3 2 C n 3 + ⋯ + n 2 C n n = n 2 n − 1 + n × ( n − 1 ) × 2 n − 2 = n ( n + 1 ) 2 n − 2 1^{2} C_{n}^{1}+2^{2} C_{n}^{2}+3^{2} C_{n}^{3}+\cdots+n^{2} C_{n}^{n}= n 2^{n-1} +n ×(n-1)×2^{n-2} =n(n+1) 2^{n-2} 1 2 C n 1 + 2 2 C n 2 + 3 2 C n 3 + ⋯ + n 2 C n n = n 2 n − 1 + n × ( n − 1 ) × 2 n − 2 = n ( n + 1 ) 2 n − 2 ②
以上是结论推导部分
这道题,我们实际需要求的是:
将①②式代入:简化答案为 ( n + 1 ) × n / 4 (n+1)×n / 4 ( n + 1 ) × n / 4 O ( 1 ) O(1) O ( 1 )
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 #include <bits/stdc++.h> using namespace std;#define pii pair<int, int> #define pdd pair<double, double> #define pll pair<ll, ll> #define debug(x) cerr << #x << ": " << x << '\n' ; #define endl '\n' typedef long long ll;typedef unsigned long long ull;int main () ll n; cin >> n; ll res = (n+1 )*n / 4 ; cout << res << endl; return 0 ; }
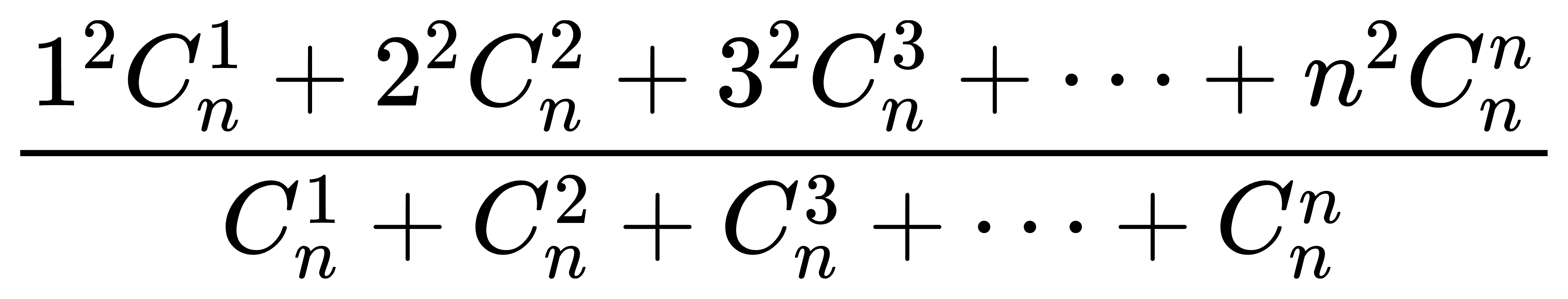






![[书生大模型]论文分类微调打榜赛二等奖-比赛方案分享](https://picbed.octalzhihao.top/img/myblog/cover/default_cover_10.webp)
